第一单元总结
在本单元中,我们完成了三次作业,第一次作业中我们要求展开所有括号,第二次作业中加入了三角函数、嵌套括号和函数调用,第三次作业中加入了求导因子。三次作业呈迭代开发关系。在整个第一单元作业中,我从始至终沿用了严格按照BNF抽象的表达式-项-因子架构,并在第一次作业中得到了100分强测分、第二次作业96分强测分、第三次作业在强测错一个点的情况下仍得到92分强侧分,有较强的化简性能。
测试方面,第二次作业及之后的每次功能添加我均使用自己编写的评测机进行超过10000条数据的黑盒测试。然而由于随机数据的覆盖不全面及评测机数据生成的偏向0的特征,仍然在第二次、第三次作业中个出现了1个bug.
由于我的程序从第一次到第三次完全呈迭代开发关系,且每次作业的添加基本没有大量修改上一次作业的内容,因此我仅从第三次完成的作业出发进行我的第一单元总结。我的总结将从以下几个方面进行
- 程序度量
- 架构设计体验
- bug分析及测试设计
- 心得体会
程序度量分析
代码行数分析
总代码行数:2024行
整体严格按照BNF定义抽象类
使用DesigniteJava.jar工具,分析得到以下数据
类分析:
| 目录 | 类 | NC | DIT | LCOM | FANIN | FANOUT |
|---|---|---|---|---|---|---|
| src | Checker | 0 | 0 | 0 | 0 | 0 |
| src | Lexer | 0 | 0 | 0 | 2 | 1 |
| src | Main | 0 | 0 | -1 | 0 | 4 |
| src | Parser | 0 | 0 | 0 | 1 | 13 |
| src | Simplifier | 0 | 0 | -1 | 6 | 7 |
| src.component | Checker | 0 | 0 | 0 | 0 | 0 |
| src.component | DFactor | 0 | 2 | 0 | 0 | 9 |
| src.component | Expr | 0 | 0 | 0.09375 | 9 | 8 |
| src.component | ExprFactor | 1 | 1 | 0.25 | 7 | 4 |
| src.component | Factor | 3 | 0 | -1 | 15 | 1 |
| src.component | FactorComparator | 0 | 0 | -1 | 4 | 1 |
| src.component | NumFactor | 0 | 1 | 0.333333 | 4 | 3 |
| src.component | Term | 0 | 0 | 0 | 6 | 7 |
| src.component | VariFactor | 0 | 1 | 0.333333 | 6 | 3 |
| src.component.function | Function | 0 | 0 | 0 | 2 | 1 |
| src.component.function | FunctionCallFactor | 0 | 0 | 0.272727 | 1 | 2 |
| src.component.function | FunctionIntaker | 0 | 0 | -1 | 1 | 7 |
| src.component.tri | CosFactor | 0 | 1 | 1 | 2 | 1 |
| src.component.tri | SinFactor | 0 | 1 | 1 | 3 | 1 |
| src.component.tri | TriFactor | 2 | 0 | 0 | 7 | 3 |
其中:
- NC表示类的子类个数
- DIT表示类所在的继承树深度
- LCOM表示内聚缺乏度,越小越好
- FANIN表示调用该类的类的个数,越大越好
- FANOUT表示该类调用的类个数
可见在我的程序中,大部分类的架构较为合理,但是抽象程度不够,可见Term和Expr的FANIN较高,这是由于他们需要调用所有Factor子类来实现对应的功能,这是不够抽象的,是由于我在设计过程中过于遵从bnf语义而躲避抽象,在避免因过度抽象导致设计困难的同时也不可避免的让Term和Expr调用了几乎所有类来实现自己的功能。
具体来说,我在Expr类中实现了自身乘其他所有类的运算方法,在Term中实现了化简方法,更为合理的设计应当将这二者独立在Expr和Term类之外,以实现高内聚低耦合。
从类深度上也可以看到,我在完成作业时最大深度仅为2,并没有足够充分的利用类的继承关系。一方面这是由于java一个类只能继承一个父类,继续抽象需要添加大量接口,而大量接口在本任务中是不必要的。另一方面可以互相继承的类在本单元任务中只因子类,因此也的确没有进一步设计的必要。
代码行数统计如下:
| 目录 | 类 | LOC |
|---|---|---|
| src | Checker | 9 |
| src | Lexer | 113 |
| src | Main | 21 |
| src | Parser | 175 |
| src | Simplifier | 349 |
| src.component | Checker | 9 |
| src.component | DFactor | 126 |
| src.component | Expr | 255 |
| src.component | ExprFactor | 57 |
| src.component | Factor | 6 |
| src.component | FactorComparator | 10 |
| src.component | NumFactor | 46 |
| src.component | Term | 348 |
| src.component | VariFactor | 64 |
| src.component.function | Function | 37 |
| src.component.function | FunctionCallFactor | 66 |
| src.component.function | FunctionIntaker | 48 |
| src.component.tri | CosFactor | 34 |
| src.component.tri | SinFactor | 34 |
| src.component.tri | TriFactor | 50 |
可以看到,在大多数类中,我的行数较为均匀,占据大量代码量的有以下几个方面:
-
Simplifier类中负责了表达式的整体展开、化简。然而随着的代码的编写,我发现一个文件的500行限制下甚至都难以放下所有的代码。该类方法行数如下:
Type Name MethodName LOC CC PC src Simplifier termToExpr 18 4 1 src Simplifier exprFactorToExpr 4 1 1 src Simplifier simplifyExpr 3 1 1 src Simplifier simplifyExpr 22 5 3 src Simplifier check1 7 2 4 src Simplifier ope1 7 1 7 src Simplifier check2 3 1 4 src Simplifier check3 3 1 4 src Simplifier ope2 17 1 7 src Simplifier ope3 18 1 7 src Simplifier check41 12 4 5 src Simplifier ope41 22 1 8 src Simplifier check51 12 4 5 src Simplifier ope51 22 1 8 src Simplifier mergeExpr 55 12 2 src Simplifier merge2Expr 53 13 2 src Simplifier canSymplifyBrace 18 5 1 src Simplifier symplifyFactor 51 12 1 其中,几个merge占用了大量的代码行数。在实现三角函数化简的过程中,我是用check/ope组合来实现具体的逻辑,这是一种比较低效的方法,以至于我不得不将剩余放不下的check/ope组合放到Term类中。这是并不优雅的做法。在反思中,我认为如果能够将各种check/ope组合使用某种规则进行抽象,应当可以减少大量的重复工作。
-
在simplifier类中放不下的化简操作被我转移到了Term中。这是一种对于优秀代码风格检查的规避行为,本不该如此。应当在接下来的课程中引以为戒。
方法复杂度分析
参考往届学长的博客【面向对象】第一单元总结 - MagicJim - 博客园 (cnblogs.com)
- Complexity Metrics
- ev(G):即Essentail Complexity,用来表示一个方法的结构化程度,范围在[1,v(G)]之间,值越大则程序的结构越“病态”,其计算过程和图的“缩点”有关。
- iv(G):即Design Complexity,用来表示一个方法和他所调用的其他方法的紧密程度,范围也在[1,v(G)]之间,值越大联系越紧密。
- v(G):即循环复杂度,可以理解为穷尽程序流程每一条路径所需要的试验次数。对于类,有OCavg和WMC两个项目,分别代表类的方法的平均循环复杂度和总循环复杂度。
- Dependency Metrics
- Cyclic:指和类直接或间接相互依赖的类的数量。这样的相互依赖可能导致代码难以理解和测试。
- Dcy和Dcy*:计算了该类直接依赖的类的数量,带***表示包括了间接依赖的类。
- Dpt和Dpt*:计算了直接依赖该类的类的数量,带***表示包括了间接依赖的类。
参考学长博客:第二次博客作业 - Inmata - 博客园 (cnblogs.com)
CogC: Cognitive complexity,认知复杂度,用来衡量代码被阅读和理解时的复杂程度。每种控制结构的使用都会增加认知复杂性,而且嵌套的控制结构越多,认知复杂性就越高。
可以通过idea插件统计分析得到如下结果:
类度量:
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| src.Simplifier | 4.277777777777778 | 14.0 | 77.0 |
| src.component.Term | 3.48 | 15.0 | 87.0 |
| src.component.DFactor | 2.3333333333333335 | 6.0 | 21.0 |
| src.component.function.FunctionIntaker | 2.2 | 5.0 | 11.0 |
| src.Parser | 2.176470588235294 | 7.0 | 37.0 |
| src.component.Expr | 2.0625 | 8.0 | 66.0 |
| src.Main | 2.0 | 2.0 | 2.0 |
| src.component.FactorComparator | 2.0 | 2.0 | 2.0 |
| src.component.tri.CosFactor | 1.6 | 4.0 | 8.0 |
| src.component.tri.SinFactor | 1.6 | 4.0 | 8.0 |
| src.Lexer | 1.5555555555555556 | 7.0 | 28.0 |
| src.component.function.FunctionCallFactor | 1.4545454545454546 | 3.0 | 16.0 |
| src.component.VariFactor | 1.4166666666666667 | 3.0 | 17.0 |
| src.component.tri.TriFactor | 1.3333333333333333 | 4.0 | 12.0 |
| src.component.ExprFactor | 1.1666666666666667 | 2.0 | 14.0 |
| src.component.NumFactor | 1.0833333333333333 | 2.0 | 13.0 |
| src.Checker | 1.0 | 1.0 | 2.0 |
| src.component.Checker | 1.0 | 1.0 | 2.0 |
| src.component.function.Function | 1.0 | 1.0 | 9.0 |
| Total | 432.0 | ||
| Average | 2.107317073170732 | 4.7894736842105265 | 22.736842105263158 |
可见,在因子方面我的实现较为合理,没有夸张的复杂度的实现。然而在Simplifier类、Term类和Expr类中,由于我试图将全部化简逻辑放在Simplifier类中,并由于文件放不下而将剩余内容放在Term类和Expr类中,导致他们的复杂度很高。另一方面,我在去除括号、合并同类项、三角函数优化等过程中大量使用instanceof关键字来分别处理,导致化简逻辑的复杂度较高。
方法度量:(筛除CogC小于1的方法)
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| src.Simplifier.mergeExpr(Expr, int) | 39.0 | 3.0 | 16.0 | 18.0 |
| src.component.Term.addSortFactor(Factor) | 38.0 | 12.0 | 15.0 | 18.0 |
| src.component.Term.merge(int) | 34.0 | 9.0 | 10.0 | 12.0 |
| src.Simplifier.merge2Expr(Expr, int) | 30.0 | 4.0 | 14.0 | 17.0 |
| src.Simplifier.symplifyFactor(Factor) | 29.0 | 11.0 | 9.0 | 13.0 |
| src.component.Term.getSpeNormal(Term, int) | 21.0 | 5.0 | 10.0 | 12.0 |
| src.component.Term.mergeSign() | 18.0 | 5.0 | 9.0 | 11.0 |
| src.component.Expr.toString() | 14.0 | 5.0 | 7.0 | 8.0 |
| src.component.Term.compareTo(Term) | 12.0 | 6.0 | 5.0 | 7.0 |
| src.Lexer.next() | 11.0 | 2.0 | 6.0 | 9.0 |
| src.component.Expr.sorting() | 11.0 | 4.0 | 6.0 | 8.0 |
| src.component.Term.toString() | 11.0 | 5.0 | 8.0 | 10.0 |
| src.Simplifier.check41(BigInteger, BigInteger, Term, Term, int) | 9.0 | 4.0 | 8.0 | 11.0 |
| src.Simplifier.check51(BigInteger, BigInteger, Term, Term, int) | 9.0 | 4.0 | 9.0 | 12.0 |
| src.Parser.parseFactor() | 8.0 | 1.0 | 8.0 | 8.0 |
| src.component.Expr.compareTo(Expr) | 8.0 | 6.0 | 5.0 | 7.0 |
| src.Simplifier.check1(BigInteger, BigInteger, TriFactor, TriFactor) | 7.0 | 2.0 | 8.0 | 11.0 |
| src.Simplifier.simplifyExpr(Expr, Boolean, int) | 7.0 | 2.0 | 5.0 | 7.0 |
| src.component.DFactor.intakeFactor(Factor) | 7.0 | 6.0 | 5.0 | 6.0 |
| src.component.DFactor.intakeTerm(Term) | 7.0 | 1.0 | 4.0 | 4.0 |
| src.component.Term.mulNum(BigInteger) | 7.0 | 1.0 | 4.0 | 5.0 |
| src.Simplifier.canSymplifyBrace(ExprFactor) | 6.0 | 5.0 | 3.0 | 5.0 |
| src.component.DFactor.intakeTriFactor(TriFactor) | 6.0 | 1.0 | 4.0 | 4.0 |
| src.component.Expr.mulExprFactor(ExprFactor) | 6.0 | 1.0 | 4.0 | 4.0 |
| src.component.tri.TriFactor.compareTo(Factor) | 6.0 | 4.0 | 4.0 | 4.0 |
| src.Parser.parseExpr() | 5.0 | 1.0 | 4.0 | 4.0 |
| src.Simplifier.termToExpr(Term) | 5.0 | 3.0 | 4.0 | 5.0 |
| src.component.function.FunctionIntaker.intakeFactor(Factor, ArrayList, ArrayList) | 5.0 | 5.0 | 5.0 | 5.0 |
| src.Parser.parseSign() | 4.0 | 2.0 | 3.0 | 4.0 |
| src.Parser.parseTriFactor() | 4.0 | 1.0 | 4.0 | 4.0 |
| src.component.Expr.mulFactor(Factor) | 4.0 | 5.0 | 5.0 | 5.0 |
| src.component.Term.sorting() | 4.0 | 2.0 | 4.0 | 5.0 |
| src.component.VariFactor.compareTo(Factor) | 4.0 | 2.0 | 3.0 | 3.0 |
| src.component.tri.CosFactor.toString() | 4.0 | 2.0 | 3.0 | 4.0 |
| src.component.tri.SinFactor.toString() | 4.0 | 2.0 | 3.0 | 4.0 |
| src.Lexer.Lexer(String) | 3.0 | 1.0 | 3.0 | 3.0 |
| src.Parser.parseNumFactor() | 3.0 | 1.0 | 2.0 | 3.0 |
| src.component.Expr.isMinus() | 3.0 | 3.0 | 2.0 | 3.0 |
| src.component.Expr.noMinusing() | 3.0 | 1.0 | 3.0 | 3.0 |
| src.component.function.FunctionCallFactor.getFunction(String) | 3.0 | 3.0 | 2.0 | 3.0 |
| src.component.function.FunctionIntaker.intakeVariFactor(VariFactor, ArrayList, ArrayList) | 3.0 | 1.0 | 3.0 | 3.0 |
| src.Lexer.getNumber() | 2.0 | 1.0 | 3.0 | 3.0 |
| src.Lexer.getTri() | 2.0 | 2.0 | 1.0 | 2.0 |
| src.Parser.parseIndex() | 2.0 | 2.0 | 2.0 | 2.0 |
| src.Parser.parseTerm() | 2.0 | 1.0 | 3.0 | 3.0 |
| src.component.ExprFactor.compareTo(Factor) | 2.0 | 2.0 | 2.0 | 2.0 |
| src.component.FactorComparator.compare(Factor, Factor) | 2.0 | 2.0 | 2.0 | 2.0 |
| src.component.NumFactor.compareTo(Factor) | 2.0 | 2.0 | 2.0 | 2.0 |
| src.component.Term.Term(Character) | 2.0 | 1.0 | 1.0 | 2.0 |
| src.component.Term.gcd(BigInteger, BigInteger) | 2.0 | 2.0 | 1.0 | 2.0 |
| src.component.Term.mergeSignTri(TriFactor) | 2.0 | 1.0 | 2.0 | 3.0 |
| src.component.VariFactor.toString() | 2.0 | 1.0 | 3.0 | 3.0 |
| src.component.function.FunctionCallFactor.compareTo(Factor) | 2.0 | 2.0 | 2.0 | 2.0 |
| src.Lexer.isFunction() | 1.0 | 1.0 | 3.0 | 3.0 |
| src.Lexer.isSign() | 1.0 | 1.0 | 2.0 | 2.0 |
| src.Lexer.isVari() | 1.0 | 1.0 | 3.0 | 3.0 |
| src.Main.main(String[]) | 1.0 | 1.0 | 2.0 | 2.0 |
| src.Parser.parseFunctionCallFactor() | 1.0 | 1.0 | 2.0 | 2.0 |
| src.Parser.parseFunctionDefinition(ArrayList) | 1.0 | 1.0 | 2.0 | 2.0 |
| src.Simplifier.check2(BigInteger, BigInteger, TriFactor, TriFactor) | 1.0 | 1.0 | 6.0 | 6.0 |
| src.Simplifier.check3(BigInteger, BigInteger, TriFactor, TriFactor) | 1.0 | 1.0 | 6.0 | 6.0 |
| src.Simplifier.ope41(int, int, Expr, Term, Term, Term, int, …) | 1.0 | 1.0 | 1.0 | 2.0 |
| src.Simplifier.ope51(int, int, Expr, Term, Term, Term, int, …) | 1.0 | 1.0 | 1.0 | 2.0 |
| src.component.DFactor.intakeExpr(Expr) | 1.0 | 1.0 | 2.0 | 2.0 |
| src.component.Expr.Expr(Expr) | 1.0 | 1.0 | 2.0 | 2.0 |
| src.component.Expr.isSorted() | 1.0 | 2.0 | 1.0 | 2.0 |
| src.component.Expr.mulTerm(Term) | 1.0 | 1.0 | 2.0 | 2.0 |
| src.component.Expr.simplified() | 1.0 | 2.0 | 1.0 | 2.0 |
| src.component.ExprFactor.toString() | 1.0 | 1.0 | 2.0 | 2.0 |
| src.component.Term.Term(Term) | 1.0 | 1.0 | 2.0 | 2.0 |
| src.component.Term.isSorted() | 1.0 | 1.0 | 2.0 | 2.0 |
| src.component.VariFactor.triToString() | 1.0 | 1.0 | 2.0 | 2.0 |
| src.component.function.FunctionCallFactor.intake() | 1.0 | 2.0 | 2.0 | 2.0 |
| src.component.function.FunctionCallFactor.toString() | 1.0 | 1.0 | 2.0 | 2.0 |
| src.component.tri.TriFactor.clone() | 1.0 | 1.0 | 1.0 | 2.0 |
正如我上文所说,我的化简部分没有进行进一步抽象,几乎所有化简都基于函数式编程的逐步操作而没有用到面向对象的抽象思想,这使得我的排序(sort)、化简(Simplify)、合并(merge)相关方法有很高的复杂度。
正如CogC指标显示,我上述方法的实现极为复杂,并且相互之间循环调用以实现自己的功能。我曾经尝试将其解耦抽象,然而我并未想到能够实现同样化简能力且成功抽象的方法,这需要我在接下来的课程中进一步学习。
类图分析
去除化简、解析相关类后,我的设计可以由如下类图表示
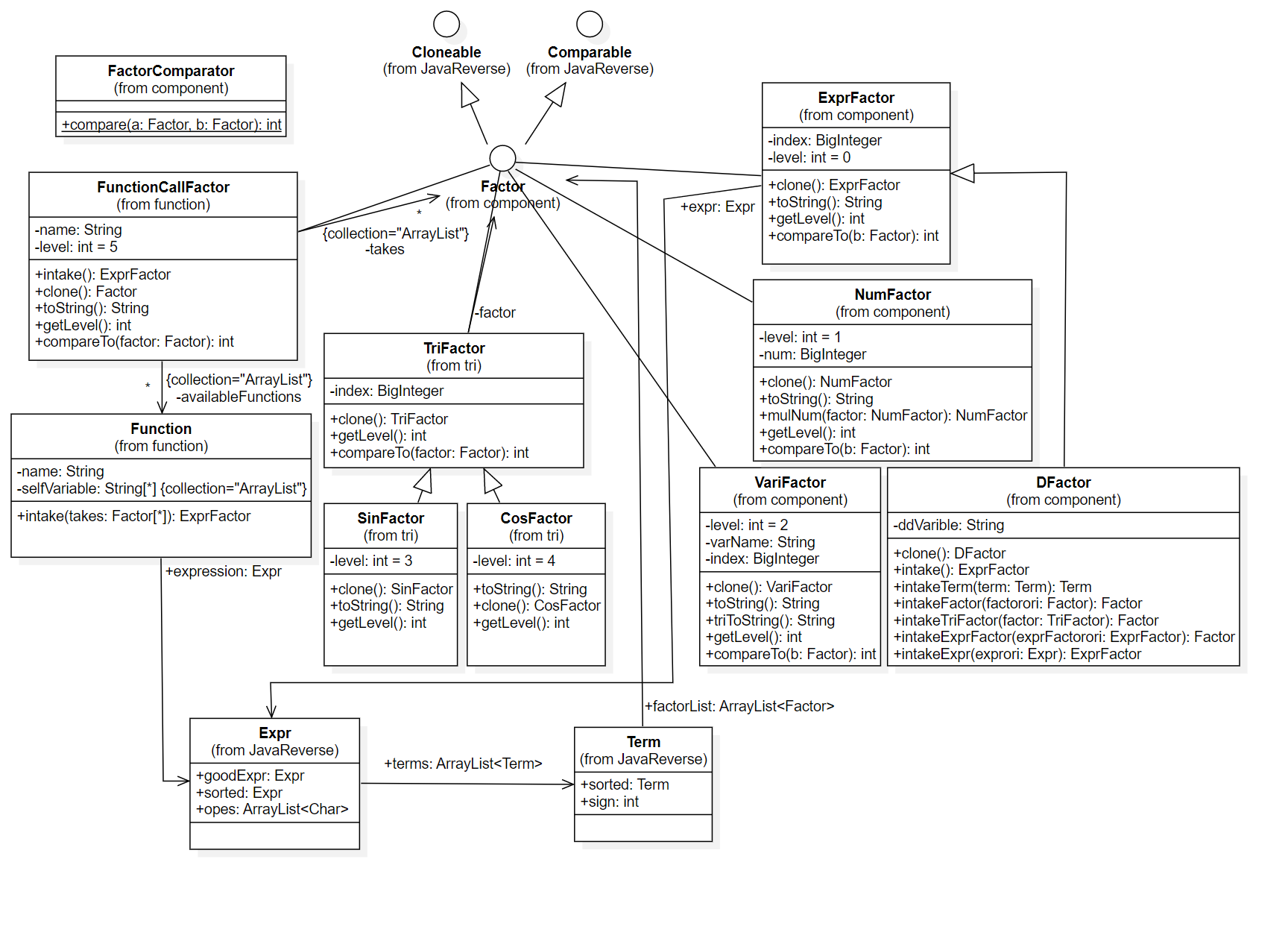
Factor作为一个重要的接口类,其继承了Cloneable和Cpmparable,力图使所有子类都具有比较的能力。
所有继承Factor类的函数都需要重写compareTo(), clone(), getLevel()函数,其中getLevel函数可以获取当前对象的排序等级,这是为compareTo服务的。由于我为每个子类都设定了唯一的等级,compareTo函数中可以使用等级值快速处理不同类的比较,其后只需要关注同类比较即可保证排序的唯一性。
可以看到,我在所有类中只使用了ArrayList数据结构,一方面这是考虑到了我将指数保存在了拥有指数的子类中,而非上层数据结构中;另一方面这是由于我力图考虑基于现有结构的迭代而非重构,并将化简逻辑与保存逻辑解耦,这使得我的表达式、项、因子相关类较为清爽。
实际上,我在化简等过程中大量使用了TreeMap和TreeSet数据结构,这是因为树结构可以避免构造hashmap,只需要实现compareTo即可且基本保证了较快的速度。
求导因子类继承了表达式因子类,这是因为他们都具有一个完整的表达式,且求导因子内部应当能够实现表达式因子内部的局部方法。又考虑到在求导因子参与其他操作时,应当表现出已经求导后的表达式的性质,因此我将带入自变量求导的相关方法作为求导因子的局部方法,供intake()方法快速调用并递归处理内部表达式。在完成后的反省中,我认为如果我能够将针对各个因子的可求导性质作为一种接口抽象并让Factor实现,从而将求导相关的逻辑分散在各种变量之中应该是一种更好的逻辑。
函数调用因子我同样作为一种因子处理。然而在本单元作业中,这种处理没有体现出更优秀的性质,这是由于本单元要求函数调用及时展开,因此我的设计中函数调用因子向外提供了intake方法并返回带入后的表达式因子,从而方便地在解析时及时调用。
三角函数因子比较简单,其中保存了一个因子和指数。在此不必过多阐述。
架构设计体验
在本单元的架构设计方面,由于我从第一次作业就彻底地坚持面向对象的思想,因此我从始至终呈迭代开发的模式不断实现新的功能,而并没有进行任何重构。
同时也由于我过于希望自己的代码能够不断迭代而放弃重构,我的代码在很多处理上依赖instanceof来进行处理,很多逻辑也都集中在了某几个工具类中,没有充分解耦,仍有很大的进步空间。
在接下来的作业中,我会进一步优化自己的架构设计,争取在减少重构的基础上提升自己架构的可扩展性,防止代码量膨胀。
bug分析及测试设计
在bug方面,在强测和互测中,我一共出现了两个bug。
- 第一个bug出现在第二次作业互测,最小样例是
sin(0)**0会错误输出0,这是由于我在化简过程中增加了sin(0)=0的特判,却没有判断指数是否是0。这反映了我对于逻辑结构的设计不够优秀,如果采用类似其他同学的优先判断指数的犯法则可以避免遇到这个bug。 - 第二个bug出现在第三次作业强测和互测,最小样例是
cos(x)*cos(y)-sin(x)*sin(y)会错误输出-cos(x+y),这是由于我在处理该类化简时设置的符号位填写错误,属于逻辑错误。由于我对于自己的代码过于自信而导致没有及时做测试残留了此bug。
第一个bug出现在Simplifier类中的simplifyFactor方法中,代码量为51行,圈复杂度为13
第二个bug出现在Simplifier类中的ope51方法中,代码量22行,圈复杂度为2
可见我的bug整体的代码量较高、圈复杂度较高。这说明在以后的程序编写中我应该尽量避免出现有复杂逻辑和循环的函数,从而使函数能够被很好的测试。
测试设计
在测试方面,我跟随课程组的假期推送及自己的一定技术积累,编写了一个基于sympy、递归下降和tkinter的多线程评测机。从理论上来讲该评测机的生成范围涵盖任意数量、组合的函数调用和表达式生成。由于为了避免过大的指数而将整数因子的范围限制到-4到4之间,除此之外理论上可以测试到所有测试点。
该测试系统的架构由生成器、tkinter串口绘制、多线程调用三部分组成。
在生成方面,该系统严格按照BNF定义递归下降生成,定义了depth参数以控制生成的表达式深度、定义了term参数以控制根表达式的项数。利用python函数也是对象的特点,在每次生成因子时生成器可以根据当前状态选择合适的生成方法加入到待随机列表中,并使用random.choice方法随机选择。因此基本可以保证测试强度。
在多线程调用部分,可以根据运行结构是否包含java报错判断re、规定时间内是否执行完成任务判断tle,有较强的自我识别能力。该评测机依靠sympy的化简功能,在测试中发生过化简后反而sympy难以识别的问题,正如课程组遇到的问题一样。这让我意识到了问题的复杂性。
该评测机的开源仓库如下:
oo_xgenerator: buaa面向对象第一单元评测机 添加一个求导、函数嵌套调用、全GUI操作、AC/WA/TLE/RE识别 (gitee.com)
内部的技术细节已在评论区发布如下:
讨论:评测机搭建——使用sympy实现自定义函数及求导 - 第三次作业 - 2023面向对象设计与构造 | 面向对象设计与构造 (buaa.edu.cn)
在互测中,评测机也发挥了一定的作用。针对大多数常见的错误及tle等问题,该评测机
然而,虽然有工具在手,仍然在第二次、第三次作业中出现了bug。尤其是第三次作业,在我新加入数据后过于依赖评测机而没有构造任何数据进行测试,这是我应该吸取的教训。
在编写评测机的同时,我接触了较多的多线程知识,至今评测机由于内部的技术栈混乱仍然难以持续稳定运行。这让我意识到技术的使用需要实践经验的积累,而积累需要尝试的勇气。
接下来的课程中,我将进一步优化自己的评测机设计思路和测试思路,吸取本单元测试设计的经验和缺陷,从而提升自己的测试水平,特别是提升自己手动构造数据的能力。
心得体会
在本单元的学习过程中,我的面向对象设计能力得到了极大的锻炼。特别是研讨课与同学的讨论使我的眼界得到了开阔,也在设计中深入使用了HashMap、TreeMap、ArrayList。对于面向对象的SOLID设计思想也有了更多的理解。
特别是理论课对于java运行时寻找匹配调用的方法的过程让我受益匪。